Tensor networks still do not perform as well on classification tasks as neural networks. This post describes an approach that improves the tensor network state-of-the-art on the MNIST and the permuted MNIST datasets.

Most of the presented results are published in Deep tensor networks with matrix product operators

Architecture

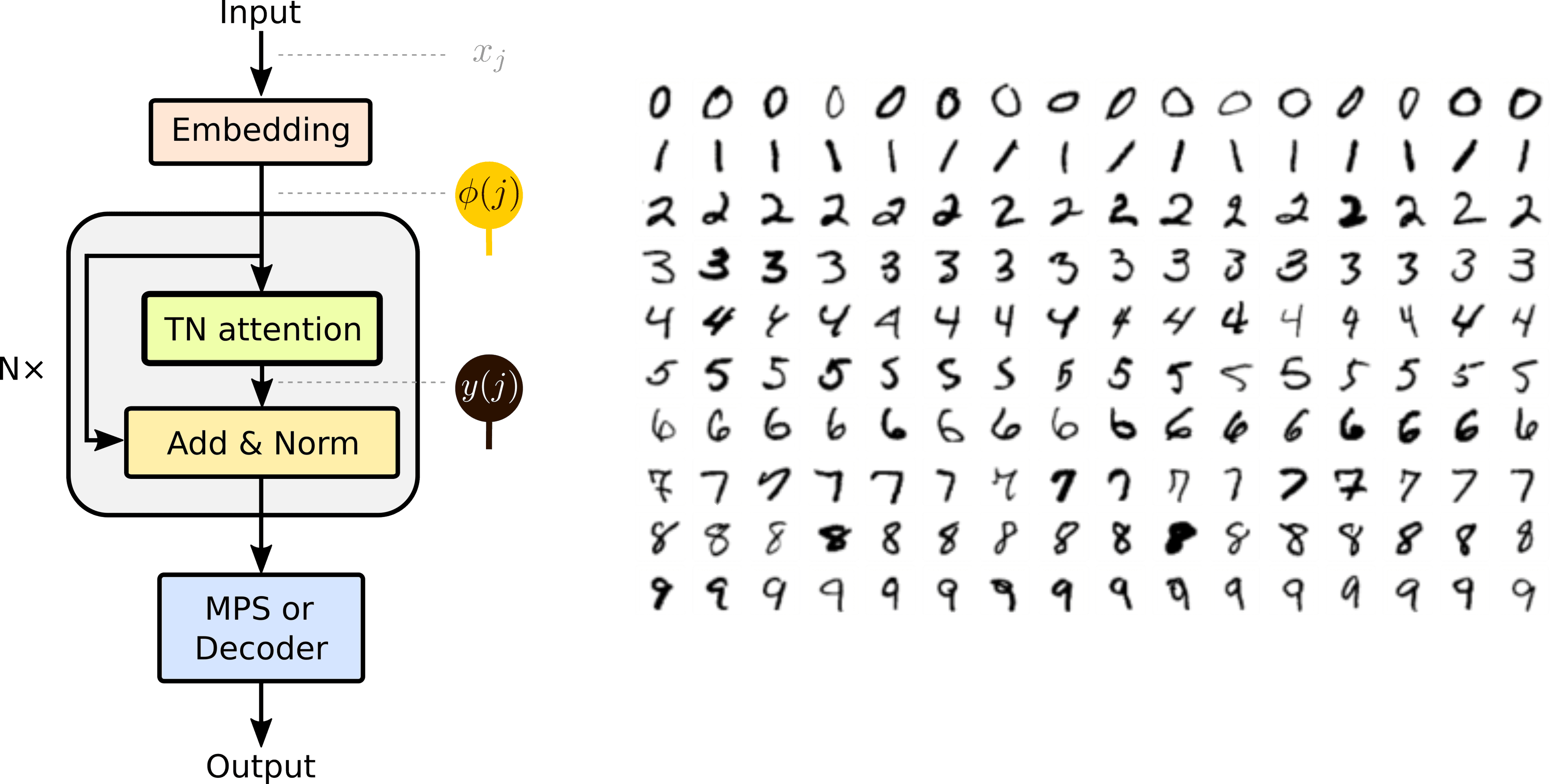
I have discussed the model architecture in a previous post on tensor network attention. For completeness, I will review the architecture in the diagrammatic notation.

The deep-tensor network has two parts. First is the embedding layer, which transforms each attribute of the input vector into a vector of size $d$. In the second part, we transform the embeddings with a series of non-linear tensor-network attention layers.

The $i$-th embedding $e_i$ is transformed by tensor-network attention by the following contraction.

The gray and the green tensors determine the left and the right context, and the blue tensor determines the local linear map. After applying the local linear map, we typically use a non-linearity, e.g., to normalize the obtained embedding and make the computation of deep tensor networks more stable.

Since the input and the output embeddings have the same size we can repeat the procedure many times. Further, each application of the tensor-network attention layer requires only $O(N)$ operations, where $N$ is the size of the input vector (or the number of embedding vectors).

Results

Let us now compare the deep tensor-network results with the MPS baselines presented in a previous post.

In the figure below, we observe the behavior of the test error on the MNIST dataset by increasing the depth of the tensor network model for three different bond dimensions of the final classifier $D_{\rm MPS}=20, 40,60$. We keep the bond dimension of the tensor network attention layer fixed $D_{\rm attention}=10$. While the error initially decreases, the training becomes more difficult for deeper networks, where the error increases. The shaded regions denote the standard deviation of the 10-fold cross-validation.

Besides a slight increase in the accuracy, we also observe slightly larger robustness to changes in the image size and the aspect ratio in the translational invariant deep tensor network models. Below we compare the robustness of uniform deep tensor networks to input aspect ratio and size changes on the MNIST dataset. The grey-shaded regions denote the training-time range of sizes and aspect ratios. Colored shaded regions show a standard deviation of the 10-fold cross-validation. At large distortions, we observe a higher accuracy in deeper models.

Finally, let us look at the accuracy of our model on the MNIST and FashionMNIST datasets and their permuted versions. In almost all cases, we observe that the deep tensor network improves the tensor-network state-of-the-art results.

We observe similar improvements also on the sequence-to-sequence classification task, discussed in detail in the referenced paper (Deep tensor networks with matrix product operators).