In this post, we dive into the variational ground-state quantum adiabatic theorem, a fascinating principle in quantum mechanics. In essence, this theorem states that, under specific adiabatic conditions, the variational ground state is preserved throughout the quantum evolution process. Beyond the theoretical interest, this concept has significant implications for near-term quantum computing.

For those interested in more technical details, feel free to check out the full paper at arXiv:2406.12392.

What Are Adiabatic Theorems?

Adiabatic theorems describe what happens when external conditions change slowly over time, such as the slow adjustment of parameters in a system’s equations of motion. A classic example is a pendulum with a length or pivot point that changes gradually. The key here is that "slow" is relative to the system's internal time scale—like the frequency of a pendulum’s swing.

When changes are slow compared to this internal frequency, many physical properties adjust just as gradually. Interestingly, some quantities—called adiabatic constants—change even more slowly, often remaining nearly constant despite large (ableit slow) changes of the system parameters.

In quantum mechanics, a similar principle applies. Consider the quantum harmonic oscillator, where the ratio of energy to frequency remains proportional to the system’s quantum number. These quantum numbers define the state of the system, and even small changes in the system’s parameters don't disrupt the "order" of these states.

Why do adiabatic constants remain stable? The mathematical reason why adiabatic constants almost do not change is perhaps surprising and is best illustraded in the case of the pendulum. It turns out (see MIT lecture) that the rate of change of the adiabatic constant of the pendulum is proportional to the difference between the potential and the kinetic energy. This difference is neither small nor slowly varying, but its average over a period is approximately zero. In fact, it becomes exactly zero when external parameters are constant. In general, the adiabatic constant remains unchanged because its time derivative depends on a rapidly fluctuating quantity, which averages out to zero over time. Consequently, the system’s overall evolution occurs on a much slower scale compared to these fast internal fluctuations, a fundamental concept in the adiabatic theorem.

Introducing the Variational Quantum Adiabatic Theorem

Now, let’s apply this to quantum systems. The variational quantum adiabatic theorem extends these ideas into quantum dynamics within a variational manifold. Think of it as a way to approximate complex quantum behavior by confining it to a simpler, more manageable space of possible solutions.

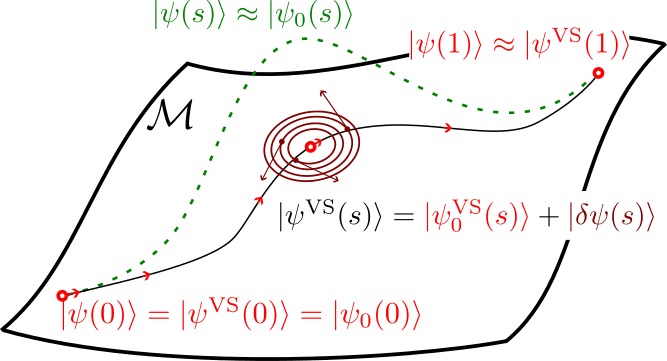
The variational dynamics of a quantum system within a parameter manifold can be visualized as follows (see figure below): Consider a Hamiltonian where both the initial and final ground states lie within the variational manifold. During the system’s full adiabatic quantum evolution (depicted by the green dashed line), the quantum state may leave the variational manifold but returns to it at the end due to adiabatic assumptions. The black line represents the variational ground state.

Now, assume that the variational state remains very close to the variational ground state throughout the process, as it starts in close proximity. Since the variational ground state is a fixed point of the dynamics (if the external parameters are not changed), we linearize the system’s behavior around it. The difference between the variational ground state and the actual state is a vector that oscillates around the ground state. These oscillations, shown as dark red ellipses, average to zero when the oscillation time scale is much smaller than the time scale associated with the slow external parameter changes. The fast oscillations of this difference are represented by large dark red arrows, while the slow evolution of the variational ground state, driven by external changes, is shown by red arrows. Therefore, the linearised evolution follows the variational gorund state and can be made arbitrary close to the actual variational evolution.

In this way, the variational ground state remains stable, providing a powerful tool for quantum computing.

Why Does This Matter?

The key takeaway from the variational quantum adiabatic theorem is that by the end of the evolution, the variational state is almost identical to the true ground state. This is crucial for quantum computing, where the final ground state often represents the solution to a computational problem.

In many quantum computing protocols, such as quantum adiabatic optimization, the system’s slow evolution through its Hamiltonian computes solutions to complex problems. And here's the exciting part: the slow change in parameters doesn’t need to grow exponentially with the size of the problem, which leads to exponential speedups in solving large-scale computations.

This suggests that similar processes could be simulated on classical computers with fewer resources, although that assumption raises some red flags. So, where’s the catch?

The Challenge of Local Minima

The assumption that brakes down in the mentioned theorem is that the variational ground state is not smooth in the variational parameters. We’re following a minimum in the variational manifold, but due to the nonlinearity of this space, multiple minima can exist. Although we start at the global minimum, changes in the parameters might cause the global minimum to become a local, less optimal, minimum — resambling a first-order phase transition in physics.

The challenge, then, is avoiding these spurious transitions. If our variational model is expressive enough to capture the exact ground state across all parameter values, we’re safe. Otherwise, we risk falling into local minima that don't represent the true ground state.

How to Avoid First-Order Phase Transitions

Several strategies can help mitigate the risk of first-order phase transitions during the variational adiabatic process - ongoing project :) .

1. Catalyst Hamiltonians: We choose the catalyst Hamiltonians as projectors onto the current variational state, potentially steering the system away from unwanted transitions.
2. Alternative Annealing Protocols: Adjusting the initial Hamiltonian or/and the initial conditions might help find a smoother path.
3. More Expressive Variational Ansätze: By enhancing the variational model, perhaps through methods like increasing the bond dimension in matrix product state (MPS) simulations, or exploring neural quantum states and parameterized quantum circuits, we improve the chances of tracking the true ground state.

Variational Quantum Adiabatic Computing

Interestingly, if we shift from real time to imaginary time, the variational adiabatic protocol turns into something closely resembling gradient descent and variational quantum eigensolvers. This connection suggests that variational quantum adiabatic computation might be used to navigate the rugged landscape of quantum optimization problems by ensuring that the closest local minimum is always the global one.

This idea holds enormous potential for improving the efficiency of variational quantum eigensolvers, one of the leading approaches for tackling real-world quantum computing problems -- another ongoing project :) .

---

In conclusion, the variational ground-state quantum adiabatic theorem offers exciting prospects for both classical and quantum computing. As we continue to refine these methods, we move closer to harnessing the full potential of quantum systems for solving complex problems in ways that were previously unimaginable.

Note: This post has been written with the aid of ChatGPT.