A popular science article published in Presek (2021, issue 3, category computer and information science) presenting a short overview of quantum machine learning. A translation of the article can be found below.

A short overview of quantum machine learning

Quantum machine learning is an interdisciplinary research field at the intersection between machine learning and quantum mechanics. To understand what quantum machine learning actually means, we will separately discuss first machine learning and then quantum computing. Only then will we look at how the fields are intertwined and why it makes sense to talk about quantum machine learning.

Machine learning is the study of algorithms for describing phenomena based on data. It is a set of algorithms that we can use to extract valuable knowledge from data as probability distributions, relations, rules, or equations. The primary feature of machine learning algorithms is independence from data interpretation. Therefore, they have become an indispensable tool in the industry, logistics, economics, medicine and pharmacy, where they are used for medical diagnostics, fraud detection, recommendation, translation, speech and font recognition, text and image classification, control of dynamic processes and systems, gaming, autonomous driving, etc. The main advantages of machine learning compared to other approaches are that they do not require domain knowledge of the problem for its successful solution and that the amount of data improves the obtained solution. In addition to more powerful computers, the rapid growth of data has enabled the latest boom in machine learning. The latter's success has further increased the need for more powerful computers, which is also the primary motivation for the accelerated development of quantum computers.

Although we could argue that all personal computers are quantum, the distinction between (classical) computers and quantum computers is still justified. The essential difference is that classical computers operate with classical information encoded in a set of zeros and ones. In contrast, quantum computers manipulate basic quantum mechanical objects, wave functions. The advantage of quantum computers then follows from the fact that the description of wave functions with the help of classical computers is very demanding. The main task of theoretical quantum computing is to find ways to express complex classical operations using the dynamics of wave functions, which we can simulate with a quantum computer. The most famous example of a classically complex procedure with a more efficient quantum algorithm is the factorization of numbers. But this, like other known quantum algorithms, needs a powerful quantum computer that can manipulate the wave function long enough, which is not yet feasible. The problem with controlling the wave function is that it must be well enough isolated from the environment, that is, the devices themselves, which change it and eventually perform the measurement. Any noise that occurs due to interaction with the surroundings spreads very quickly and corrupts the desired algorithm. Current devices are not suitable for known quantum algorithms that require many quantum operations. The opposite is true with machine learning, adapted to work with large amounts of noisy data. Machine learning algorithms thus represent a natural (appropriate) application of current noisy quantum computers.

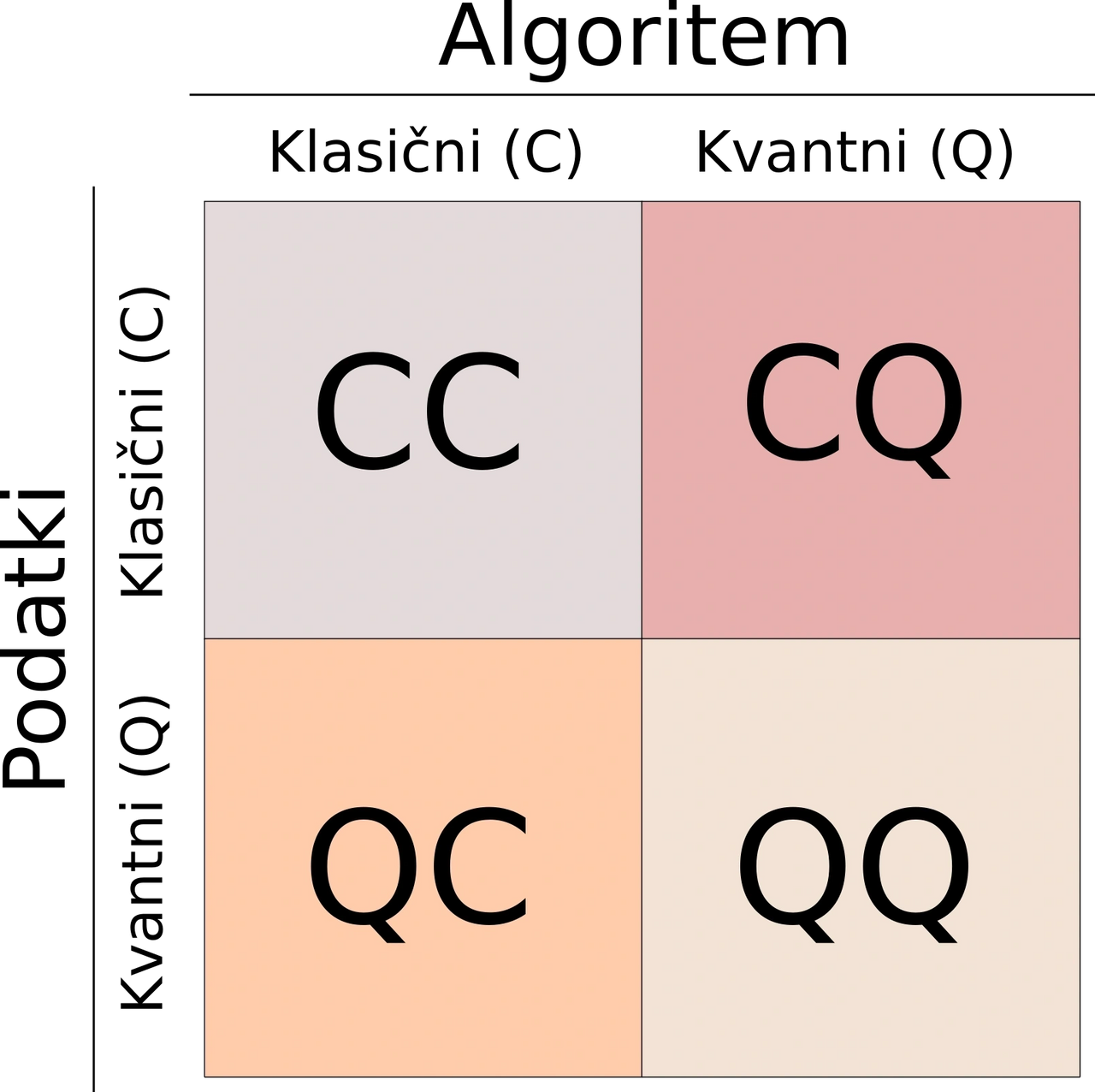
The joint applicability of machine learning and quantum computing has encouraged the transfer of ideas between fields. In particular, using quantum computers to accelerate classical machine learning algorithms and the latter's transfer to the quantum domain. We also see a general broadening of both fields in terms of new theoretical tools, questions, and interpretations typically reserved for the other field. The research field of quantum machine learning can be divided into four sub-fields according to the algorithm (classical or quantum) and data (classical or quantum), as shown in the cover image.

It is least intuitive that describing classical data with classical algorithms falls within quantum machine learning. This includes research that uses methods from one area to solve problems in another research area. For example, quantum state compression methods can also be used to compress deep neural networks. This has a very high practical value due to the transfer of deep neural networks to computationally less powerful devices. The same methods can also solve typical machine learning problems, such as classification, new data generation, or translation.

On the other hand, classical machine learning methods such as Boltzman machines, neural networks, and autoregressive models started to be applied to describe complex quantum systems. Machine learning models are also helpful in detecting phase transitions. This first sub-field of quantum machine learning can also include the classification of the expressiveness of neural networks using methods for the classification of quantum states and other formal connections between the concepts of machine learning and quantum mechanics.

However, machine learning algorithms are not only helpful in processing classical data but also quantum ones. In this area, we can highlight two uses of machine learning. The first is the calibration of the experiments. These are minor adjustments to the experimental devices so that they are correctly calibrated. In many experiments with quantum systems, this is a very time-consuming process that can be automated by machine learning. In addition to calibration, machine learning is also helpful in determining the wave function or quantum tomography. Quantum tomography deals with how we can most effectively measure the state of a quantum system (wave function). The number of measurements we have to take to determine the state of a quantum system increases very rapidly with its size. Therefore, quantum tomography of multi-particle quantum systems is a challenging problem where machine learning can significantly reduce the number of measurements required.

The most active area of ​​quantum machine learning is the use of quantum computers to solve machine learning problems. A quantum computer is used as a computational accelerator (similar to a GPU or TPU) that implements a sequence of quantum gates with multiple parameters. These parameters, similar to standard machine learning of neural networks, are adjusted according to the input data. In addition to optimising quantum gate parameters, the coding of classical information into a quantum state and measurements are also critical in this approach. Despite the availability of quantum devices, the described process is very demanding.

Nevertheless, quantum computers have already been used to solve easier machine learning problems, such as digit classification (MNIST). Although these problems are elementary from the point of view of standard machine learning methods, we must point out that the performance of quantum algorithms increases rapidly with the size of quantum computers. This has been growing in recent years, so it is tough to predict when quantum algorithms will be more successful than classical ones.

The last sub-field of quantum machine learning, quantum data processing with quantum algorithms, is still in its infancy. This includes tasks such as processing the results of quantum experiments or assisting in quantum cryptography. The advantage of this approach is the direct manipulation of the wave function without an intermediate measurement step, where we can lose a lot of information due to the presence of noise.

The presented sub-fields of quantum machine learning are intertwined and complementary. New findings also affect other broader fields, such as physics, chemistry, bio-informatics and pharmacy. The applicability and generality of quantum machine learning are the main reason for the growing interest of researchers and the general public in quantum machine learning, which promises an exciting future.